|
Music Studio |
|
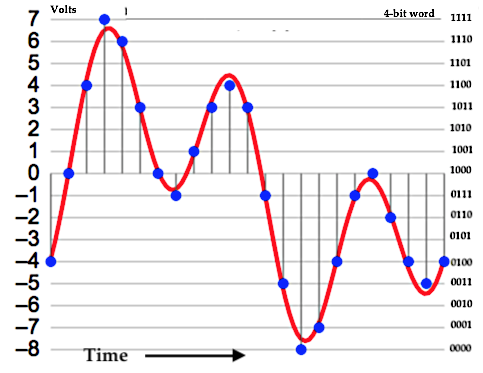
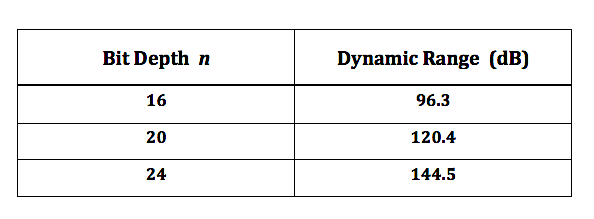
Some time ago, we looked at the various audio signal levels through the analog portion of the signal path. Here, we’ll take a look at signal levels in the digital signal processing realm. The range of signal levels that can be recorded is limited by the finite number of quantized voltage levels available in the analog-to-digital conversion process. This finite number is determined fully by the bit depth used for the binary word that labels each of the quantized voltage levels. Let’s refer back to the example used previously to describe the digitization of an analog signal In the figure, the analog signal voltage varies in time, going almost equally above and below zero volts. Over a sufficiently large time window, the time-averaged voltage tends to zero for actual complex signal waveforms. So, we’ll just focus on the positive voltage excursions above the zero-volts horizontal axis. In this example, a n = 4 bit word is used for the binary number labels. The most significant bit (MSB) in this word is the leftmost digit, which is “1” for positive voltages 0 to +7 volts . (The MSB is “0” for negative voltages.) If we ignore this MSB “sign bit” , notice that the remaining binary word ranges from “000” to “111”, yielding 8 discrete voltage levels for positive voltages. So the largest amplitude (loudest sound) voltage that can be recorded is given by: The smallest amplitude (softest sound) voltage that can be recorded occurs halfway between the “000” and “001” levels, since this voltage will be rounded up and recorded at the “001” level. Any voltage less than this “halfway” voltage will be rounded down to 0 volts (silence), or equivalently, is masked by the quantization noise. Dynamic Range Dynamic range is defined as the ratio between the loudest and quietest sounds that can be recorded. Given a bid depth of n, the dynamic range of a digital audio recording can be expressed, using |Vmax| and |Vmin| from above, as Let’s calculate the dynamic range using the formula in (3) for the example in the figure above, For bit depth n = 4, Dynamic Range = 24.08 – 1.09 = 22.99 dB . Now do a check by substituting the max and min voltages in (1) and (2) directly in (3), giving which is in very good agreement with the previously calculated value. In actual practice, bit depths are fairly large, n > 10 . Therefore, we can drop the negligibly-small second term on the right-hand side of equation (3), and we get the well-known formula for dynamic range in digital audio, Here are the theoretical values of dynamic range for the bit depths commonly used for recordings. In the next post, we’ll address how to ‘measure’ the signal amplitude level in the digital domain.
Comments are closed.
|
Categories
All
Archives
May 2023
|

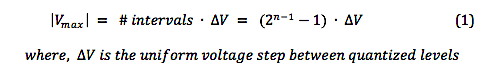

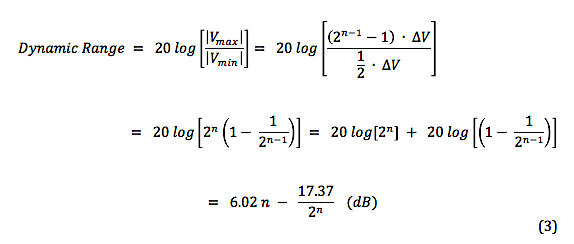
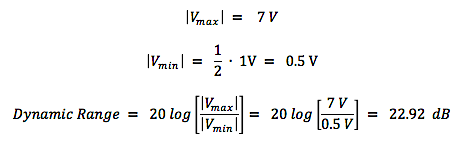
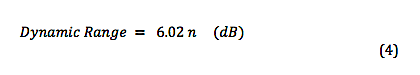
 RSS Feed
RSS Feed
